3D Sternbilder
Die Idee für diese Spielerei kam mir, als ich nach Weihnachtsgeschenken suchte. Verschenkt als Tannenbaumschmuck macht sich das ganz gut: selbstgebastelt, mit Köpfchen und steht nicht das ganze Jahr über im Weg :-P
Viel Spaß beim Basteln!

Hintergrundwissen
Die Sterne des Nachthimmels sind keine Diamanten auf dunklem Seidentuch oder nur weiße Punkte am runden Himmelszelt. Sie sind riesige brennende Gasbälle verstreut in der Nähe um unser eigenes Sonnensystem. Fast alle liegen näher als 150 Parsec (490 Lichtjahre), dh. sie liegen uns direkt vor der Nase im Bezug auf die Größe unserer Galaxie. Trotzdem sind sie für unsere Augen weit weg und wir können ihre Entfernung nicht wahrnehmen. So sehen wir nur eine Projektion der Sterne auf eine Kugeloberfläche, die die Erde umspannt. In dieser Projektion meinen wir manchmal Figuren zu erkennen: Die Sternbilder.
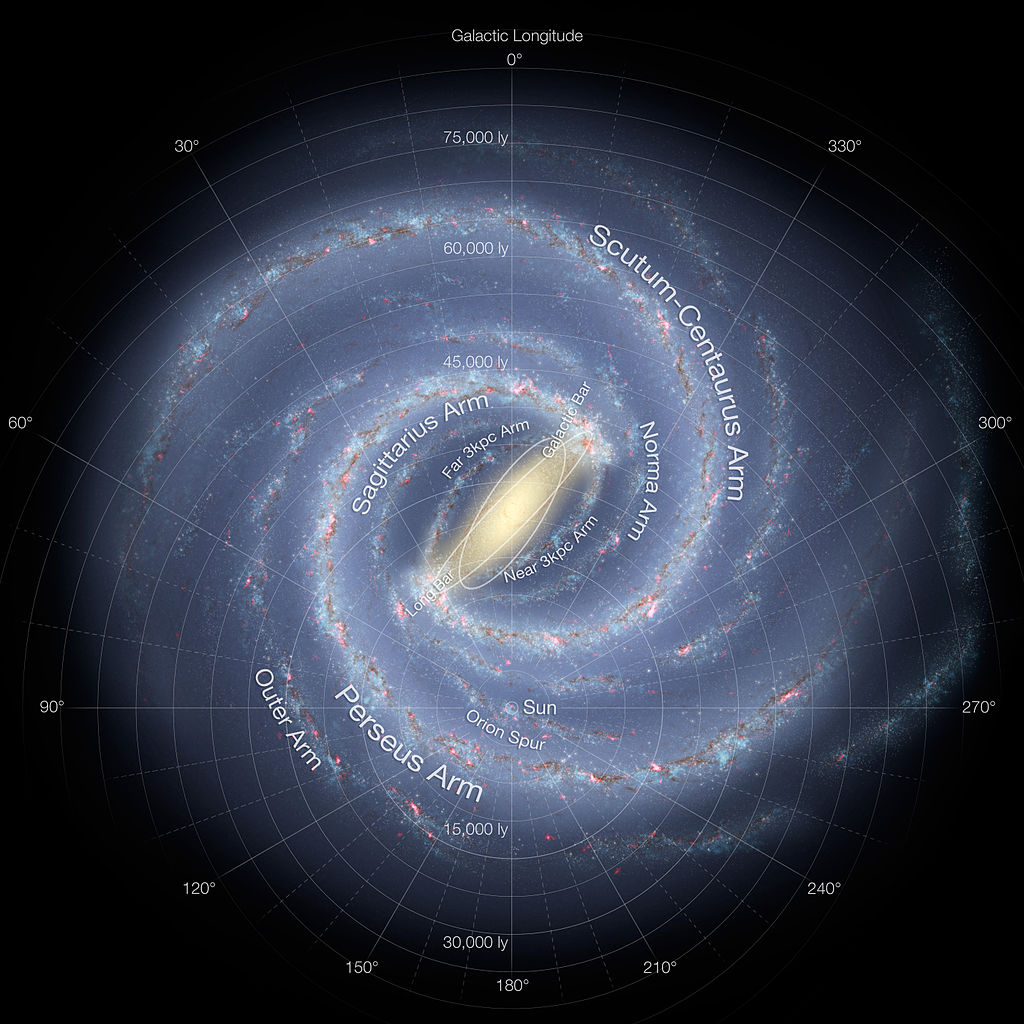 Wir sind innerhalb unserer eigenen Galaxie und können daher kein
Foto von ihr aufnehmen. Dieses Bild zeigt die Milchstraße, wie
sie wohl aussähe, wenn wir von außen darauf schauen könnten.
Alle unsere Sternenbilder liegen innerhalb des Orionarms.
Wir sind innerhalb unserer eigenen Galaxie und können daher kein
Foto von ihr aufnehmen. Dieses Bild zeigt die Milchstraße, wie
sie wohl aussähe, wenn wir von außen darauf schauen könnten.
Alle unsere Sternenbilder liegen innerhalb des Orionarms.
Sternenbilder gibt es in vielen Kulturen und unsere westlichen Sternbilder stammen von altgriechischen und arabischen Sternkonstellationen ab. Welche Sterne zum Bild nun dazugehören und welche nicht, ist eine eher willkürliche Festlegung, die an vielen Stellen anders gezeigt wird. Du darfst selber entscheiden, ob du dein Sternbild verändern möchtest, eine antike Variante raussuchst, oder ein offizielles Bild von der International Astronomical Union (IAU) verwendest.
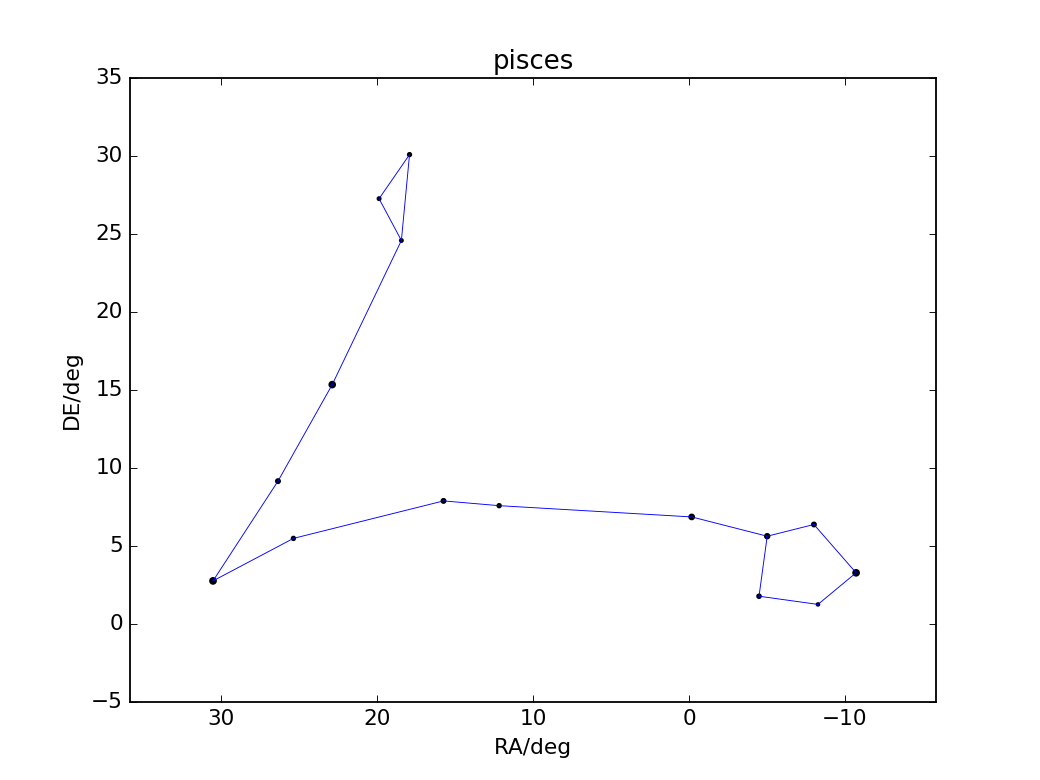
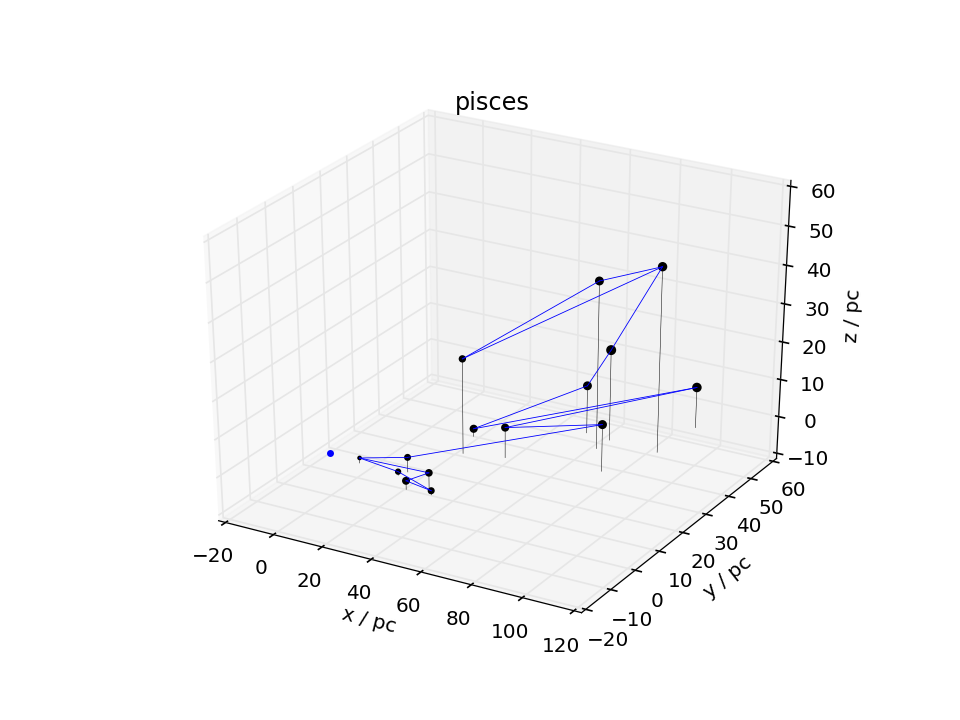
Betrachten wir die dreidimensionale Position der Sterne fällt auf, wie weit sie eigentlich von einander entfernt liegen, obwohl sie am Himmel nah beisammen erscheinen. Das wollen wir bei dieser Bastelei handfest veranschaulichen.
 |
 |
Mathematik
In den Sternkatalogen wird die Sternposition im Äquatorialen Koordinatensystem angegeben: Die Rektaszension (RA, $\alpha$) und Deklination (DE, $\delta$) sind sozusagen die Höhen- und Breitengrade in der Astronomie. Für eigentlich alle Sterne in den Sternbildern ist die Parallaxe $p$ bekannt. Aus ihr lässt sich die Entfernung $d$ des Sterns berechnen: \[ \begin{align} p &= \tan{\frac{1\mathrm{AU}}{d}} \\ \equiv d &= \frac{1\mathrm{AU}}{\arctan{p}} \overset{p \ll 1^\circ}{\approx} \frac{1\mathrm{AU}}{p} \end{align} \] Die Entfernung, die eine jährliche Parallaxe von einer Bogensekunde hervorruft, ist gerade ein Parsec (etwa 3.26 Lichtjahre). In den Katalogen wird die Parallaxe oft in Millibogensekunden (mas, milliarcseconds) angegeben: \[ d[\mathrm{pc}] = \frac{1000}{p[\mathrm{mas}]} \]
Nun haben wir alles, um die Positionen in ein kartesisches Koordinatensystem umzurechnen: \[ \begin{align} x &= d \cdot \cos\alpha \cdot \cos\delta \\ y &= d \cdot \sin\alpha \cdot \cos\delta \\ z &= d \cdot \sin\delta \end{align} \] Hier zeigt die x-Achse in Richtung des Frühlingpunktes (Frühlings-Tagundnachtgleiche), die y-Achse in Richtung der Sommersonnenwende und die z-Achse liegt entlang der Rotationsachse der Erde.
Die Entfernung $c$ zwischen Sternen an den Positionen $(x_1, y_1, z_1)$ und $(x_2, y_2, z_2)$ ist nach dem Satz des Pythagoras: \[ c = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} \]
Kataloge
Ich habe die Daten aus dem Hipparcos-Katalog (FTP) verwendet, dem ersten großen Datensatz mit präziser Astrometrie von 1997. Wer keine ordentlichen Angaben über Messunsicherheiten braucht, kann auch den HYG-Katalog (GIT) nehmen, der etwas mehr allgemein interessante Informationen enthält. Für coole Leute gibt’s jetzt den neuen Gaia-Datensatz (FTP) von 2016! Der ist aber eigentlich zu umfangreich :-D
Nicht-Programmierer können die Sterne auch auf der Wikipedia nachschlagen (zB. Gamma Piscium) und die Daten aus den Infokästen raussuchen.
Mehr Zahlen
Wo wir schon dabei sind, wissenschaftliche Daten zu verarbeiten, können wir noch einen drauf legen: Ich habe die Helligkeit und Farbe der Sterne durch unterschiedlich große und farbige Sterne abgebildet.
Die Helligkeit der Sterne wird häufig in Magnituden angegeben und bezieht sich auch auf die Farbe: Ein rötlicher Stern ist im roten Spektrum heller als im blauen Teil seines Spektrums. Außerdem bedeutet eine größere Magnitude, dass der Stern dunkler ist (etwas gewöhnungsbedürftig...). Für unsere Augen ist der Stern in seiner scheinbaren Helligkeit $V$ im sichtbaren Spektrum zu sehen. Dabei heißt $V=0\mathrm{mag}$ dass der Stern so hell ist, wie der Stern Vega im Sternbild Leier, der Polarstern Polaris (Dreifachstern) hat $V=1.97\mathrm{mag}$ und unsere Sonne $V=-26.74\mathrm{mag}$. Mit dem Auge sind Sterne unter guten Bedingungen bis $5\mathrm{mag}$ oder $6\mathrm{mag}$ sichtbar.
Weiter entfernte Sterne erscheinen natürlich dunkler als nähere Sterne. Wenn wir die Entfernung $d$ eines Sterns kennen, können wir seine absolute Helligkeit $V_{abs}$ berechnen. Dies ist die Helligkeit des Sterns, die man beobachten würde, wenn man genau $10\mathrm{pc}$ von ihm entfernt wäre: \[ V_{abs} = V - 5\mathrm{mag} \cdot \log_{10}\frac{d}{10\mathrm{pc}} \]
Die Farbe eines Sterns können wir durch den Farbindex $B-V$ beschreiben, der größer ist, je rötlicher ein Stern ist. Unsere Sonne hat den Wert $B-V=0.65$ und Vega hat $B-V=0.00$
Daten sammeln
Als erstes musst du dich für eine Sternkonstellation entscheiden. Ich habe die Fische und die Waage nach den offiziellen IAU-Konstellationen gebastelt. Wenn du nicht programmieren möchtest, kannst du die Daten auf der Wikipedia nachschlagen und die Berechnungen "per Hand" durchführen. Sonst musst du nun die Katalognummer (zum Beispiel HIP 114971) herausfinden. Dazu habe ich Stellarium verwendet. (Achtung: Die Sternbilder sind dort etwas, anders.) Auch die Katalognummern sind auf der Wikipedia aufgeführt.
Danach kannst du aus deinem Katalog die Sterne anhand der Katalognummer heraussuchen und $\alpha,\,\beta,\,p,\,V$ und $B-V$ auflisten.
Außerdem müssen wir noch einen Maßstab wählen: Ich habe für die Längen $0.2\frac{\mathrm{cm}}{\mathrm{pc}}$ genommen. Es hat sich herausgestellt, dass es auch sinnvoll ist die Winkel $\alpha$ und $\delta$ zu skalieren (ich hab sie verdoppelt), da das Modell sonst zu schmal wird. Dadurch werden Verzerrungen eingeführt, die stärker sind, je näher die Sterne an den Polen liegen. (Dort treffen sich alle Deklinations-Linien in einem Punkt.) Nunja ...
Python
Ich habe dafür ein Python-Skript verwendet, das du in diesem Ordner finden kannst. Wenn du den Hipparcos-Katalog herunterlädst und eine CSV-Datei mit folgenden Spalten erstellst, macht es die restliche Arbeit:
- HIP Katalognummer
- Verbindungen: Eine Liste von anderen Katalognummern getrennt durch einfache Leerzeichen.
- Name des Sterns
- Mythologischer Name (optional)
- Mehr Beschreibung vom Stern (optional)
Beispiel:
7097,8198,η Psc,Kullat Nunu,double star
Eine Beispieldatei ist auch in dem Ordner. Dann das Skript ausführen mit
python3 constellations.py -c hip_main.dat -o Pisces pisces.csv
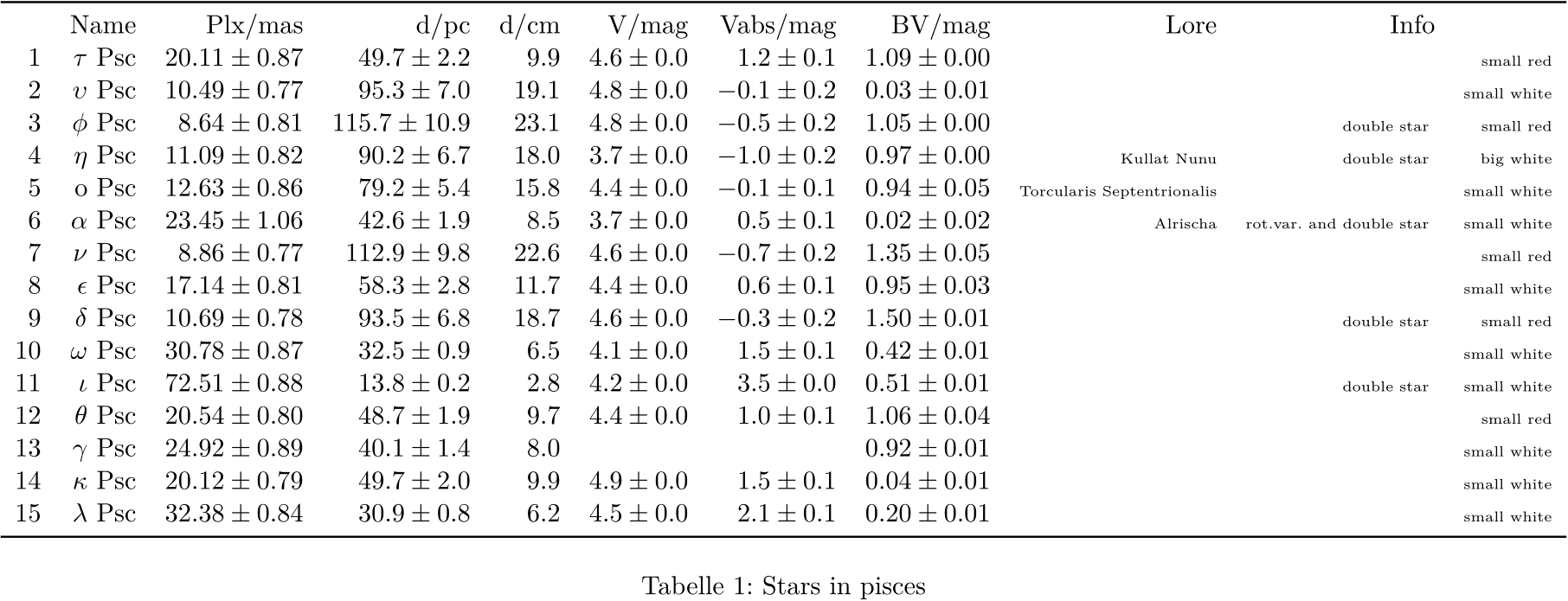
und es werden CSV-Dateien mit Infos über die Sterne und Verbindungen angelegt, sowie Diagramme in 2D und 3D erzeugt. Die CSV-Dateien dann einfach in dein Lieblings-Tabellenprogramm importieren und zB. ausdrucken.
 |
 |
Basteln
Wie immer lohnt es sich, die Anleitung erst ganz durchzulesen, bevor du Anfängst, um unliebsame Überraschungen zu vermeiden ;-) Genauso wichtig ist es, der Anleitung nicht kopflos zu folgen, denn deine eigenen Anpassungen sind bestimmt an einigen Stellen erforderlich.
Materialien & Werkzeug
- Geschenkband mit 5mm Breite in rot, weiß und blau,
- Messingdraht mit 1mm Durchmesser
- Jeans-Garn in weiß
- Sekundenkleber, der durchsichtig klebt
- Schere
- Seitenschneider
- Spitzzange
- Permanentmarker
- Schraubenzieher mit dünnem Schaft (1mm Durchmesser)
- besonders kleine Lampe (zB Handy-Taschenlampe)
Natürlich kannst du gerne auch breiteres Geschenkpapier, anderen (vorzugsweise weniger biegsamen) Draht und anderes Garn verwenden. :-D
Schritt 1: Sterne
Aus dem Geschenkband werden die Fröbelsterne gebastelt. Dafür gibt es viele Anleitungen im Internet für einige Varianten. Einfach mal Googlen, oder diese nehmen
Wie gesagt: Ich habe unterschiedlich große Sterne für unterschiedliche $V_{abs}$ und unterschiedlich farbige für unterschiedliche $B-V$ gemacht. Für Mehrfachsternsysteme habe ich weitere kleine Sterne in der gleichen Farbe hergestellt (auch wenn die Begleitsterne eigentlich eine andere Farbe haben) und zusammengeklebt.
 Das sind alle Sterne, die ich für die Sternbilder Fische und
Waage gebastelt habe. Dazu der Messingdraht unten rechts. Den
Silberdraht habe ich am Ende doch nicht verwendet.
Das sind alle Sterne, die ich für die Sternbilder Fische und
Waage gebastelt habe. Dazu der Messingdraht unten rechts. Den
Silberdraht habe ich am Ende doch nicht verwendet.
Schritt 2: Draht formen
Erst musst du dich entscheiden, wie du den Draht durch dein Sternbild legst. Die Fische lassen sich aus einem einzelnen Draht formen, die Waage aber nicht (da habe ich die Verbindungslinie zwischen $\gamma$-Librae und $\alpha$-Librae als Knotenpunkte mit einem zweiten kurzen Draht ergänzt.
An den Stellen, an denen ein Stern ist, habe ich einen Kringel in den Draht gemacht, damit eine wohldefinierte Knickstelle entsteht. Außerdem lässt sich dort das Garn für die Verbindung zur Erde einfädeln und Verbindungenen mit anderen Verbindungsdrähten herstellen. Aber Achtung: Ist der Draht erstmal so eng gebogen, bricht er wahrscheinlich, falls du versuchsts ihn zurückzubiegen!
Für die Kringel und Knotenpunkte ist ein wenig Köpfchen gefragt, damit die Kringel ordentlich aussehen. Wenn du nun weißt, wo dein Draht im Sternbild entlang laufen soll, kannst du ein Stück abmessen und mit dem Marker markieren:
- 4cm Anfang (wird später abgeknipst)
- 1cm für Anfangs-Kringel
- Wiederhole für jeden Stern:
- Verbindungslinie zum nächsten Stern
- 1cm für den Kringel
- 4cm Ende (wird später abgeknipst)
Anschließend zB in der Mitte damit anfangen die Sterne aufzufädeln und nach und nach die Kringel zu biegen und dabei schonmal möglichst genau die richtige Form zu erreichen. Ein paar Tipps:
- Um Kringel zu machen, wickle den Draht mindestens einmal um einen abgeschnittenen Rest von gleichem Draht. So hat der Kringel die richtige Größe, um andere Verbindungsdrähte hindurchzustecken.
- Versuche schon beim Formen von Kringeln, die Knotenpunkte sind, auf deren Orientierung zu achten, sodass sich die Verbindungsline senkrecht dazu einfach durchstecken lässt.
- Stelle Knotenpunkte von mehreren Drähten her, indem du einen Draht durch den Kringel vom anderen Steckst und darum einen Kringel machst. Dann verrutscht nichts mehr.
- Achte genau darauf auf welcher Seite vom Kringel du den Stern auffädelst: Du solltest ungehindert das Garn vom Kringel zur "Erde" spannen können.
Nicht die Konzentration verlieren, denn Zurückbiegen schwächt oder bricht den Draht! :-P
Schritt 3: Sichtlinien
Aus einem weiteren Stück Draht kannst du einen Aufhänger herstellen, indem du eine Schlaufe legst, verzwirbelst und in das andere Ende einen Haken biegst. Die Schlaufe stellt die Erde dar.
Mit dem Jeans-Garn werden nun die Verbindungslinien gezogen: Messe so viel Garn ab, wie der Stern im Modell von der Erde entfernt ist, und gebe mindestens 8cm für die Handhabung hinzu. Mache dann einen festen Knoten (ich habe 5 verdrehte halbe Schläge übereinander gelegt) in einen Kringel mit Stern. Mache einen einfachen halben Schlag in die Öse der Erde und lege das ganze an ein Lineal, bevor du den Knoten ganz fest machst. Hier ist noch höhere Genauigkeit gefragt!
Ich habe gerade so viele Sterne mit der Erde verbunden, dass das Modell stabil hängt. Je mehr Sichtlinien du einfügst, umso mehr andere fangen an locker herumzuschlabbern, denn so genau kann bestimmt niemand mit der Hand arbeiten.
 |
 |
Schritt 4: Ausrichten
Im letzten Schritt werden die Modelle getrimmt, sodass sie möglichst genau die echten Sternbilder wiedergeben. Dazu projezieren wir das Sternbild mit einer Taschenlampe, die genau an die Stelle der Erde gehalten wird, auf einen Tisch. Je kleiner die Lichtquelle ist, umso schärfer werden die Schatten der Sterne.
Auf dem Tisch sollte nun eine Gnomonische Projektion des Sternbilds zu sehen sein. Nähere Sterne werfen größere Schatten. Biege den Draht nun vorsichtig So, dass ein ordentliches Abbild zu erkennen ist.
 |
 |

Herzlichen Glückwunsch, deine Sternkonstellation ist fertig!
Formeln: MathJax
